Analizando datos de Spotify con Análisis de Componentes Principales en R: Los Planetas

Después de descargar datos sobre Los Planetas de Spotify en la publicación anterior, en esta ocasión vamos a aplicarles análisis de componentes principales (PCA, por sus siglas en inglés: Principal Component Analysis).

Sin entrar en detalle, PCA es una técnica de reducción de dimensionalidad, esto es, permite resumir las variables de un conjunto de datos en nuevas variables (llamadas componentes principales) que sintetizan gran parte de la información original.

Preparación: paquetes y carga de datos

library(dplyr)       # Para el uso de pipes (%>%)
library(FactoMineR)  # Para realizar PCA
library(factoextra)  # Para visualizar PCA
library(ggplot2)     # Para visualización de datos
library(ggrepel)     # Para repeler geometrías de ggplot2

# Cargamos los datos generados anteriormente en:
# https://danielredondo.com/blog/2021-08-27-spotify_planetas/
load("canciones.RData")

Vemos la estructura de los datos, y renombramos las columnas más relevantes que usaremos en el análisis.

str(canciones)

## tibble [109 x 13] (S3: tbl_df/tbl/data.frame)
##  $ id              : chr [1:109] "02jXZfT8IjNmdrKbnHBq1J" "0e8EpWgw3MmmY1641BiFWG" "0eOEe1eGVaxNhLFDrQqp5H" "0h84bQDr2i0uLzTRfQuEt5" ...
##  $ name            : chr [1:109] "Islamabad" "La Maquina de Escribir" "Corrientes Circulares En El Tiempo" "Entre Las Flores Del Campo (Caracoles)" ...
##  $ album_id        : chr [1:109] "1khQHoHWfemMaJpmxCMaqJ" "4qNag8cUD12cazCepgfZ6O" "2yr7ln77nOyA7RzE6T4X4I" "165G43fsCZWFPm6zH1caLN" ...
##  $ album           : chr [1:109] "Zona Temporalmente Autónoma" "Pop" "Encuentros con entidades" "La Leyenda Del Espacio" ...
##  $ duration        : num [1:109] 423 343 278 163 236 ...
##  $ tempo           : num [1:109] 118 133 123 138 138 ...
##  $ valence         : num [1:109] 12.8 53 54.7 39.6 73.5 82.2 55.7 66.5 91.1 46.5 ...
##  $ danceability    : num [1:109] 36.4 25.5 52.3 34.2 48.3 36.6 17 15 61.1 28 ...
##  $ energy          : num [1:109] 51.6 93 78.3 65.7 85.7 94.9 88.2 82.3 82.8 68.6 ...
##  $ acousticness    : num [1:109] 33.9 0.1 0.1 0 2.5 2.1 0 0.1 14.2 5.5 ...
##  $ instrumentalness: num [1:109] 28.7 2.5 82.1 6.4 0 73.8 0 0.4 0.4 65.6 ...
##  $ liveness        : num [1:109] 10.5 18.8 12.7 13 4.9 69 29.3 19.5 11.4 22.6 ...
##  $ speechiness     : num [1:109] 3.5 7.6 3 4.5 4.5 4.5 5.3 4 2.8 4 ...

names(canciones)[5:12] <- c("Duración", "Tempo", "Positiva", "Bailable",
                            "Enérgica", "Acústica", "Instrumental",
                            "En directo")

PCA

La función PCA del paquete {FactoMineR} realiza la reducción de dimensionalidad y devuelve la posición de los datos y variables originales en el nuevo espacio de dos dimensiones.

# Extraemos dos componentes principales con los datos escalados y
# pedimos que no muestre los gráficos (son muy simples, y
# los vamos a mejorar más adelante)
pca <- FactoMineR::PCA(canciones[5:12], scale.unit = TRUE,
                       ncp = 2, graph = FALSE)

Mostrando un resumen, podemos observar que las dos primeras componentes principales explican el 51% de la varianza total. Si considerásemos 3 componentes principales, explicarían el 64% de la varianza, y con 4 componentes tendríamos explicada el 75% de la varianza.

summary(pca)

## 
## Call:
## FactoMineR::PCA(X = canciones[5:12], scale.unit = TRUE, ncp = 2,  
##      graph = FALSE) 
## 
## 
## Eigenvalues
##                        Dim.1   Dim.2   Dim.3   Dim.4   Dim.5   Dim.6   Dim.7
## Variance               2.178   1.901   1.038   0.883   0.815   0.602   0.354
## % of var.             27.221  23.761  12.972  11.041  10.184   7.523   4.427
## Cumulative % of var.  27.221  50.982  63.954  74.995  85.179  92.702  97.129
##                        Dim.8
## Variance               0.230
## % of var.              2.871
## Cumulative % of var. 100.000
## 
## Individuals (the 10 first)
##                  Dist    Dim.1    ctr   cos2    Dim.2    ctr   cos2  
## 1            |  3.318 | -2.361  2.348  0.506 | -1.331  0.855  0.161 |
## 2            |  1.870 |  0.591  0.147  0.100 |  1.176  0.668  0.396 |
## 3            |  2.090 |  0.428  0.077  0.042 | -0.280  0.038  0.018 |
## 4            |  1.658 |  0.588  0.146  0.126 | -0.188  0.017  0.013 |
## 5            |  2.262 |  1.934  1.577  0.732 | -0.300  0.043  0.018 |
## 6            |  3.356 |  0.707  0.211  0.044 |  0.442  0.094  0.017 |
## 7            |  2.249 |  0.808  0.275  0.129 |  1.499  1.084  0.444 |
## 8            |  3.645 |  0.658  0.182  0.033 |  2.464  2.930  0.457 |
## 9            |  3.058 |  2.031  1.737  0.441 | -1.529  1.128  0.250 |
## 10           |  1.295 | -0.927  0.362  0.513 |  0.431  0.090  0.111 |
## 
## Variables
##                 Dim.1    ctr   cos2    Dim.2    ctr   cos2  
## Duración     | -0.633 18.377  0.400 |  0.357  6.701  0.127 |
## Tempo        |  0.110  0.551  0.012 |  0.626 20.608  0.392 |
## Positiva     |  0.824 31.190  0.679 | -0.164  1.423  0.027 |
## Bailable     |  0.436  8.730  0.190 | -0.683 24.567  0.467 |
## Enérgica     |  0.641 18.883  0.411 |  0.651 22.278  0.423 |
## Acústica     | -0.427  8.375  0.182 | -0.653 22.466  0.427 |
## Instrumental | -0.490 11.022  0.240 |  0.179  1.687  0.032 |
## En directo   | -0.250  2.871  0.063 |  0.072  0.271  0.005 |

El siguiente gráfico nos va a ayudar a interpretar el análisis realizado:

# Para mejorar la visualización, cambiamos una opción del paquete {ggrepel}
# para que haya un máximo de 3 puntos superpuestos.
set.seed(314) # Semilla para reproducibilidad en {ggrepel}
options(ggrepel.max.overlaps = 3)

# Gráfico PCA general
fviz_pca_var(pca, col.var="contrib",
             gradient.cols = c("royalblue", "blue", "darkblue"),
             repel = T) +
  # Opciones del gráfico
  theme_classic() +
  theme(title = element_blank(),
        text = element_text(size = 14))

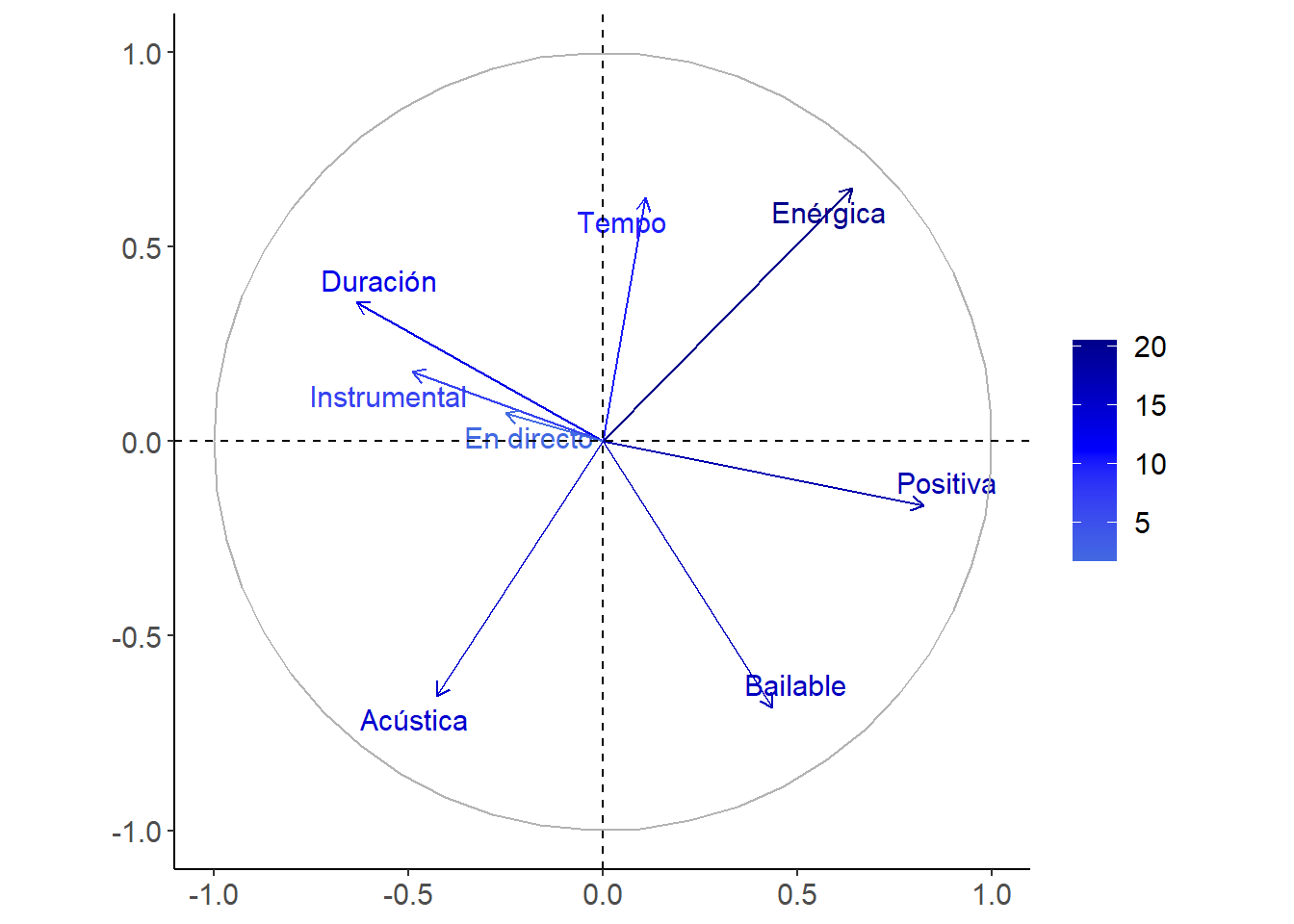
Al aplicar PCA, la información ha sido redimensionada a un espacio de 2 dimensiones, donde cada flecha señala la ubicación en este nuevo espacio de cada una de las características originales. A la vista de este gráfico, podemos extraer algunas conclusiones como las siguientes:

• Las canciones instrumentales y las canciones largas son bastante similares.
• Las canciones acústicas y las canciones enérgicas están en polos opuestos.
• Las canciones positivas son más cortas, y en general no son instrumentales, ni grabadas en directo.

A continuación, podemos representar las canciones en el gráfico, dando el mismo símbolo a canciones que pertenecen al mismo álbum.

# Gráfico PCA por álbum
fviz_pca_biplot(pca, repel = TRUE, col.var = "blue",
                geom.var = c("arrow", "text"),
                label = "var", habillage = factor(canciones$album)) +
  # Opciones del gráfico
  theme_classic() +
  theme(title = element_blank(),
        text = element_text(size = 14))

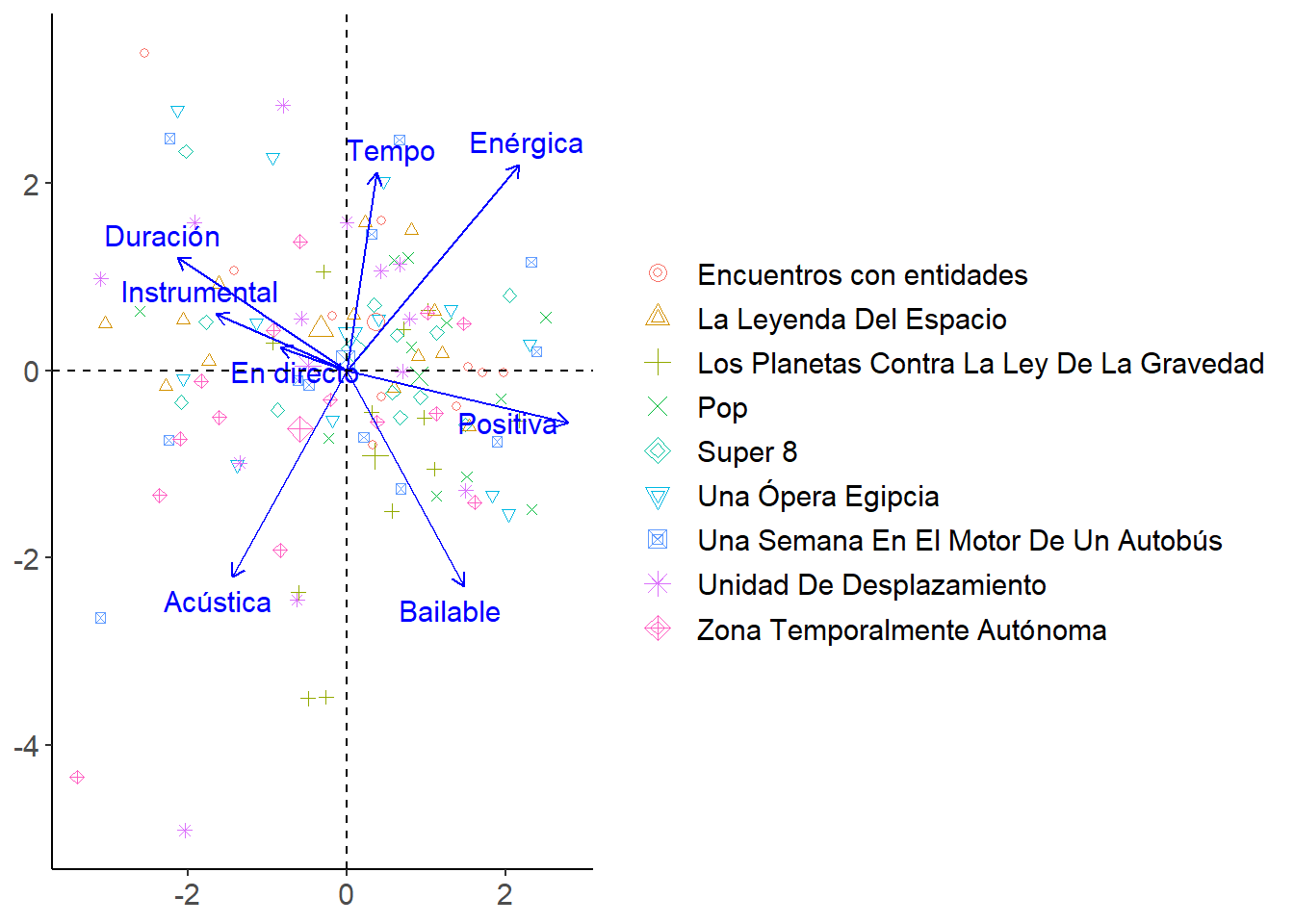
Ahora vamos a destacar algunas canciones que se encuentran en los bordes del gráfico.

# Cambiamos la opción para ggrepel para que se puedan superponer más puntos
options(ggrepel.max.overlaps = 5)

# Enseñando algunas canciones sueltas
rownames(pca$ind$coord) <- canciones$name
fviz_pca_biplot(pca, label = c("ind", "var"), repel = TRUE,
                col.ind = "gray50", col.var = "blue", geom = "point") +
  # Se etiquetan algunas canciones
  geom_label_repel(mapping = aes(x = pca$ind$coord[,1], y = pca$ind$coord[,2],
                                 label = rownames(pca$ind$coord)),
                  color = alpha("black", .5),
                   label.size = NA, fill = NA) +
  # Opciones del gráfico
  theme_classic() +
  theme(title = element_blank(),
        text = element_text())

En este gráfico, las canciones que están cerca son parecidas teniendo en cuenta las componentes principales. Mirando por ejemplo en la parte inferior izquierda, tenemos “Hay una estrella” y “Línea 1”. En la esquina superior izquierda tenemos canciones largas cargadas de psicodelia como “Dulces sueños”, “Los poetas” y “La Copa de Europa”.

Este ejercicio visual se podría realizar de forma objetiva aplicando técnicas de clustering para encontrar grupos de canciones similares entre sí. Pero en lugar de ello, vamos a hacer más atractiva la visualización de los resultados obtenidos con PCA.

Gráfico interactivo de PCA

Vamos a realizar un gráfico para poder representar de forma interactiva las componentes principales, la transformación de cada variable, y la ubicación en ese nuevo espacio de todas las canciones. Usaremos para ello el paquete {highcharter}. Aunque aquí el código se pone más técnico, el resultado de la visualización merece la pena.

library(highcharter) # Para hacer gráficos interactivos

# Se extraen las nuevas coordenadas de cada canción
df <- tibble(
  canciones$name,
  pca$ind$coord[, 1], pca$ind$coord[, 2])
names(df) <- c("cancion", "PCA1", "PCA2")

# Se representan las canciones
hchart(df, "point", hcaes(x = PCA1, y = PCA2, group = cancion),
       color = "darkblue", legendIndex = 140) %>% 
  # Títulos de los ejes
  hc_yAxis(title = list(text = "PCA2")) %>% 
  hc_xAxis(title = list(text = "PCA1")) %>% 
  # Añadir estilo al gráfico
  hc_add_theme(hc_theme_ft()) %>% 
  # Leyenda a la derecha con los nombres de todas las canciones
  hc_legend(align = "right", verticalAlign = "top", layout = "vertical") %>% 
  # Opciones del gráfico
  hc_plotOptions(
    line = list(
      marker = list(
        enabled = F, symbol = "triangle", enabledThreshold = 0,
        fillColor = "black", lineWidth = 2, lineColor = "black"
      )
    )
  ) -> grafico

# Se añaden las variables una a una
for(i in 1:8){
  grafico <- grafico %>% 
    hc_add_series(data = rbind(c(0, 0), pca$var$coord[i,]), type = "line",
                  color = rainbow(8)[i], lineWidth = 3,
                  name = rownames(pca$var$coord)[i], legendIndex = i)
}

# Se muestra el gráfico
grafico

Todo el código de R utilizado para esta publicación está disponible en este repositorio de GitHub. ¡Os invito a analizar las canciones de vuestros grupos favoritos!